Simplexní metody a jejich použití v digitálním zpracování signálů
Úvod
Adaptivními systémy nazýváme systémy jejichž parametry se mění v čase, většinou, v závislosti na vstupním signále. Budeme-li tedy hovořit o adaptivních filtrech, budeme mít na mysli filtry jejichž koeficienty jsou proměnné v čase a závisí na vlastnostech vstupního signálu.
Tyto systémy nacházejí uplatnění v široké škále aplikací. Jde například o aplikace rozpoznávání řeči, v expertních systémech, automatických řídících systémech, měřící technice a, v neposlední řadě, v telekomunikacích.
V adaptivní filtraci se setkáváme se třemi základními úkoly:
Ať již mluvíme o jakékoli úloze, vždy se algoritmus implementovaný do systému snaží odhadnou vlastnosti vstupního signálu a pomocí filtru s proměnnými koeficienty tento signál modelovat. Při odhadu parametrů signálu algoritmus vychází z účelové funkce, kterou se snaží minimalizovat. Jedná se vlastně o hledání minima na N rozměrném chybovém povrchu.
Tento N-rozměrný povrch lze popsat funkcí J o N proměnných. Hledání minima funkce J je hledání bodu, kde je gradient funkce J nulový. Z této podmínky dostaneme, derivací funkce J, soustavu N rovnic. Pro klasické úlohy - estimaci respektive predikci - se tato soustava nazývá Wiener-Hopfovy, respektive Yule-Walkerovy, rovnice. Soustava N rovnic se dá, v podstatě, řešit dvěma způsoby:
Přímé metody jsou metody vedoucí k výsledku v konečném počtu kroků. Jsou to například: Gausova eliminace, výpočet inverzní matice nebo metoda LU rozkladu. Přímé metody se dají použit pouze pro lineární rovnice. Výhodou je předem známý počet kroků. Problém může nastat s výpočetní náročností pro velká N.
Iterační metody jsou metody založené na zpřesňování výsledku v každém následujícím kroku. Přesnost výsledku závisí na počtu iterací a nelze přesně říci kolik kroků bude k dosažení výsledku potřeba. Mezi tyto metody patří například: metoda prosté iterace, Newtonova metoda či gradientní metoda. Pro lineární metody lze použít i Jacobiovu metodu či Gauss-Seidelovu metodu. Výhodou těchto metod je možnost řešení nelineárních rovnic. Nevýhodou je neznámý počet kroků vedoucích k výsledku.
Dosud uvedené metody řeší rovnice, jejichž koeficienty jsou konstantní. V adaptivní filtraci však dochází ke změnám koeficientů během iterace. Pokud iterační metoda konverguje rychleji, než se mění analyzovaná funkce J, může vést k výsledku. Touto oblastí se v matematice zabývají nelineární iterační metody.
Další problém může nastat ve chvíli, kdy funkce J nemá pouze jedno minimum, ale má několik lokálních minim. Iterační metody pak mohou uvíznout v lokálním minimu a globálního minima nikdy nedosáhnout.
Problém nalezení globálního minima libovolné funkce bez zadání okrajových podmínek není dosud uspokojivě vyřešen. K řešení tohoto problému se používají nelineární iterační metody, které můžeme rozdělit do dvou kategorii:
Derivací využívají metody gradientní. Ty však nemohou řešit problémy, kdy se nedá určit derivace funkce J. Pro takové problémy nám zbývají metody prohledávající: simplexní metody, genetické či Powllova metoda. Tyto metody se většinou oužívají v kombinaci s okrajovými podmínkami, kdy je zadána množina na které se má minimum hledat.
Gradientní metody se chovají lépe v okolí minima a podávají přesnější výsledky. Mají však sklon uvíznout v lokálním minimu. Prohledávající metody jsou, naopak, odolnější vůči "zabloudění", ale jejich chování kolem minima je horší. Proto se v praxi používá kombinace prohledávajících metod s metodami gradientními. V prvním kroku se pomocí prohledávajících metod lokalizuje přibližně poloha minima a v druhém kroku se toto minimu nalezne přesně pomocí gradientních metod. Tento postup bývá, jak již bylo uvedeno, doplněn okrajovými podmínkami - tedy množinou vymezující prohledávanou oblast.
Nyní se budeme zabývat simplexními metodami.
Simplexní metody
Princip simplexních metod publikovali v roce 1964 panové J.A. Nelder a R. Mead.
Metoda slouží k minimalizaci libovolné funkce o N proměnných bez použití derivací této funkce.
Metoda spočívá v posouvání vrcholů N úhelníka (např. trojúhelníka - v trojdimenzionálním prostoru) podle jistých pravidel směrem k minimu. Pravidla by se, zjednodušeně, dala shrnut do čtyř pohybů: reflexe, expanze, kontrakce a sražení. Reflexe je myšlené přenesení nejvyššího (a tudíž nejhůře položeného) bodu souměrně k těžišti tělesa. Pokud je tato poloha nejnižší ze všech ostatních, dochází k definování nového bodu na místě dvojnásobné vzdálenosti od těžiště tělesa. Tento pohyb se nazývá expanze. Pokud je reflektovaná poloha nejvyšší, dochází ke kontrakci - umístění vrcholu uprostřed mezi původní vrchol a těžiště. Pokud je i po kontrakci uvažovaný vrchol nejvyšší, dochází ke sražení - všechny vrcholy se posunou směrem k nejnižšímu o polovinu.
Algoritmus vypadá následovně:
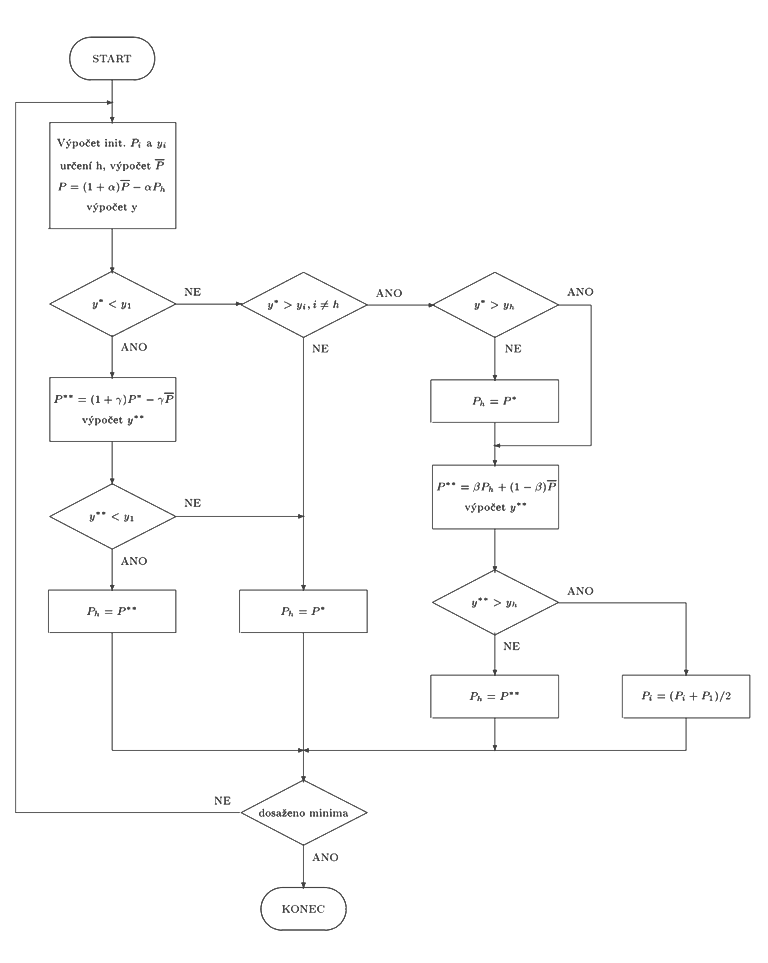
písmeno P označuje vrchol obrazce, y je hodnota v bodě P, index "l" značí nejnižší, "h" nejvyšší hodnotu. P s čárou značí těžiště brazce.
Volba strany obrazce určuje robustnost vůči uvíznutí v lokálním minimu a chování algoritmu v okolí minima. Algoritmus konverguje relativně rychle. Rychleji než např. Powllelův algoritmus.
Možnosti využití v oblasti zpracování signálu
Oblast využití simplexních algoritmů je široká. Dá se využít všude tam, kde je potřeba minimalizovat funkci N proměnných. V oblasti zpracování signálů se jedná o minimalizaci chybové funkce. Pokud se jedná o zpracování v dávkovém módu, kdy není požadavek na rychlost, dá se použít bez problémů. Ty nastanou ve chvíli, kdy je požadavek na zpracování v reálném čase.
Nicméně i přes tuto nevýhodu se objevují pokusy aplikovat tyto metody v adaptivní filtraci. Například pánové H.Strik a L.Boves aplikovali tento algoritmus na odhad parametrů řeči pro čtyřparametrový Fantův model řeči.
Další aplikace je např. při řešení inverzního problému v EEG, kdy se ze znalosti rozložení potenciálového pole, na povrchu hlavy, snažíme určit polohu dipólu, jenž toto pole generuje. Zde se minimalizuje funkce:
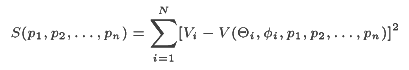
tedy minimalizujeme rozdíl mezi naměřenými potenciály a potenciály generovanými dipólem o příslušných parametrech. Vzhledem k tomu, že distribuce potenciálu na povrchu hlavy není jednoznačná, omezuje se prohledávaná plocha na čtvrtinu hlavy, kde se předpokládá výskyt zdroje vyvolaného určitým podnětem.
V této aplikaci se využívá kombinace simplexního algoritmu s algoritmem Marquardtovým, což je algoritmu gradientní a poskytuje větší přesnost nalezení minima. Další informace o této aplikaci lze najít např. v práci pánů Gevinse a Remonda.
Použité zdroje
K tvorbě této stránky jsem použil:
[1] zápisky z přednášek Prof.Ing.P.Sovky,CSc.
[2] J.A. Nelder, R. Mead: A simplex method for function minimalization, Compter Journal, vol.7,1964
[3] H.Strik, L. Boves: Automatic estimation of voice parameters
[4] Gevins, A.S., Remond A.: Methods of Analysis if Brain Electrical and Magnetical Signal, EEG Handbook, 1987